Un gabarit d'angle pour guide d'affûtage : méthode géométrique

Note : le bouton ![]()
(ci-dessus) n'est pas actif.
Par Sébastien Gros
La distance de saillie du tranchant par rapport au rebord du guide peut se déduire d’après une équation qui permet de la calculer pour un angle donné :
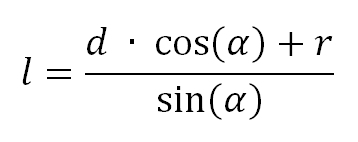
En revanche, la résolution est loin d’être intuitive si on souhaite retrouver l’angle correspondant à une distance donnée !
Pour retrouver l’angle ⍺ à partir de la distance l, on peut, afin de simplifier les calculs et obtenir un résultat somme toute très proche de la réalité, se résoudre à poser deux approximations :
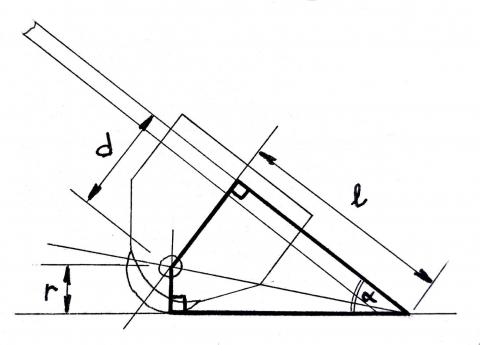
- la première consiste à considérer que l’axe de la roulette se trouve à l’aplomb du milieu de la largeur des mors.
- la seconde se base sur un constat : l’appui du guide se fait non pas dans le prolongement de la bissectrice de la largeur des mords qui passe par l’axe de la roue, mais bien au point de contact de la roulette sur le plan d’appui (le rayon de la roulette étant limité en comparaison de la dimension du guide, l’approximation reste cohérente). Nous allons considérer que le rayon de la roulette a une incidence négligeable sur l’angle d’affûtage. Notez que pour les valeurs d’angle qui nous intéressent, l’approximation reste valable, mais plus l’angle d’affûtage est élevé, plus l’erreur induite par cette approximation sera importante.
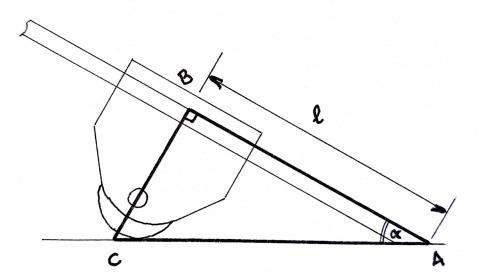
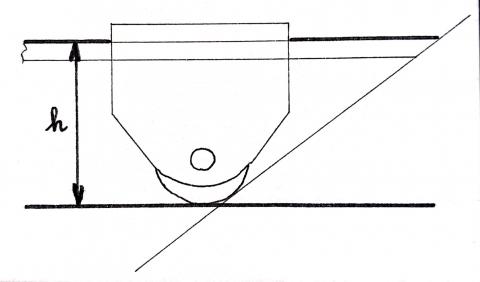
D’une part, l’angle d’affûtage (l’angle ⍺ que fait la lame avec l’abrasif) représente un des angles du triangle rectangle du schéma ci-dessus. D’autre part, on est capable de déterminer par la mesure la distance (h) qui sépare le plan de maintien de la lame dans le guide et le plan de l’abrasif sur lequel le guide repose en position verticale. On est alors en mesure de déterminer la longueur du côté opposé de notre triangle rectangle.
On peut alors s’appuyer sur les relations trigonométriques dans un triangle rectangle pour retrouver la valeur du côté adjacent AB, c’est-à-dire la longueur l :
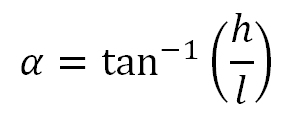
La valeur de la distance de la butée au rebord du guide est obtenue en soustrayant de cette valeur la moitié de la largeur des mors.
Alors j’en conviens, c’est tout de même théorique et un peu rébarbatif ! D’ailleurs on n’a pas attendu de connaître les relations trigonométriques pour affûter des tranchants. La méthode pratique présentée dans l'article, qui s’appuie sur le rapporteur de menuisier, permet de déterminer avec une excellente précision la distance qui correspond à l’angle d’affûtage que l’on souhaite et ce sans s’arracher le moindre cheveu ni se faire le moindre nœud au cerveau.

























Vos commentaires